The speed at which an object must travel in order to escape from the object which it is orbitting [sic].
The Apollo 11 spacecraft had to travel at least 7 miles per second (11.25 km/s) to break free of Earth's gravitational field. This speed is 32.4 times as fast as the speed of sound (“Mach 32.4"). The fastest military plane, the SR-71 Blackbird, travels (only) Mach 3.
I can
remember watching live coverage of the Apollo missions, and the newscasters
would make similar statements, which always bothered me. I knew that gravity
got weaker as you went up, and I couldn’t figure out why a certain speed was
required to "break free." As it turns out,
you don’t need to achieve escape velocity in a powered ship.
Let’s do a
little thought experiment. Let’s say you
are in a powered space craft with an advanced propulsion system of virtually
unlimited energy (e.g. nuclear fusion) so that fuel is not a consideration
(this is a physics discussion, not engineering). You decide to start traveling towards the
moon at a speed less than escape velocity.
What is going to stop you? Where
is the “brick wall” you must break through?
Gravity won’t
be your problem. It will be getting
weaker the further you go. The weight FH of
the ship at a given height H is given by (See the Appendix for details of this
calculation):
Where R is
the radius of the earth and Fs is its weight at the surface.
Let’s look at
an example of how the original weight of a ship (let’s say 10 tons) changes as
you move from the surface of the Earth (height=0) to the moon (height=238,900
miles).
The
International Space Station orbits at a height of about 250 miles. At that height the weight of your ship has
only decreased about 10%. However, as
you go up the weight really starts to drop off.
By the time you are 10% of the way to the moon your weight has dropped by
more than half. Halfway to the moon your
ship weighs about 21 pounds, or 0.1% of its original weight.
As we see,
if you have a powered ship and don’t have to worry about fuel, the power
required to go to the moon drops off quite rapidly. If we are going along a modest clip of 1000
mph, we will get to the moon in about 10 days, and the job will get a lot easier as we go along.
So, where
does escape velocity come in? To answer
that, it helps to understand how escape velocity is defined.
The definition of escape velocity is: neglecting air
friction, how fast does an unpowered object have to be going to
coast
away from a celestial body, and never fall back. For example, a projectile
fired from the surface of the moon at the moon's escape velocity would coast away and
never fall back.
Calculating escape velocity is very straightforward using some basic calculus. If you integrate the
work required to lift a body an infinite distance away from a celestial object
(say the earth), and then equate that value to the kinetic energy of a projectile, and solve for velocity you
get the following equation for escape velocity (for the earth in this case):
Note that escape velocity is
defined in terms of unpowered objects. Our example
involves a powered spacecraft of virtually unlimited energy. Escape velocity is not relevant to our desire
to go to the moon. You can go as slow as you like.
Achieving escape velocity is sufficient to get to the moon,
but not necessary. It also turns out
that due to the limited energy of today's rocket fuels it is a convenient
engineering practice to achieve escape velocity. In no sense is it necessary from the
standpoint of physics.
Appendix: Calculations for those who care:
The force of
gravity on your ship is given by:
Where:
G = the gravitational constant
Me = the mass of the Earth
Ms = the mass of the ship
R = the radius of the Earth = 3,959
miles = 6,371 km
H = the height above the surface
Note that
what we call weight is the force of gravity acting on your mass. For simplicity we will stick with weight
since that is what we observe in our daily life.
What is the change in the weight as you go up? We will calculate it as a ratio of weight at a height h (FH) versus weight at the surface (Fs).
Solving for the
weight at a given height FH yields:

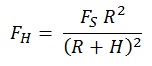





No comments:
Post a Comment